from sympy import symbols, Eq, solve4 เงินรายงวดพื้นฐาน (Basic Annuities)
พื้นฐานบทนี้ใช้ความรู้เรื่องอนุกรมเรขาคณิต (Geometric Series)
- แบบจำกัดจำนวนพจน์ (Finite Geometric Series) \[ S_n = a + ar + ar^2 + \dots + ar^{n-1} = a \cdot \frac{1 - r^n}{1 - r}, \quad r \ne 1 \] และ \[ S_n = ar + ar^2 + \dots + ar^{n-1} + ar^{n}= a \cdot r\cdot \frac{1 - r^n}{1 - r}, \quad r \ne 1 \]
\(a\) = พจน์แรก
\(r\) = อัตราส่วนร่วม
\(n\) = จำนวนพจน์
- แบบอนันต์ (Infinite Geometric Series) \[S = a + ar + ar^2 + ar^3 + \dots = \frac{a}{1 - r}, \quad \text{เมื่อ } |r| < 1\]
4.0.1 การใช้ซิมไพ สำหรับอนุกรมเรขาคณิต
อนุกรมเรขาคณิต (Geometric Series) คืออนุกรมที่พจน์ถัดไปแต่ละพจน์เกิดจากการคูณพจน์ก่อนหน้าด้วยค่าคงที่ \(r\) ซึ่งเรียกว่า “อัตราส่วนร่วม” ตัวอย่างเช่น อนุกรม \(a, ar, ar^2, ar^3, \dots\)
อนุกรมเรขาคณิตแบบจำกัดจำนวนพจน์
from sympy import Sum, oo, symbols
# กำหนดตัวแปร
a, k, r, n = symbols('a k r n')
# อนุกรมเรขาคณิตแบบจำกัดจำนวนพจน์
finite_sum = Sum(a * r**k, (k, 0, n - 1))
finite_sum # ไม่ต้องหาผลรวม\(\displaystyle \sum_{k=0}^{n - 1} a r^{k}\)
คำสั่งด้านบนเป็นการสร้างอนุกรม \(\sum_{k=0}^{n-1} ar^k\) โดยยังไม่คำนวณผลรวมจริง แต่แสดงในรูปแบบสัญลักษณ์ หากต้องการคำนวณหาผลรวมของอนุกรม สามารถใช้คำสั่ง .doit() ซึ่งจะให้ผลลัพธ์ในรูปสมการปิด (closed-form) ตามสูตรทางคณิตศาสตร์
finite_sum.doit() # หาผลรวม\(\displaystyle a \left(\begin{cases} n & \text{for}\: r = 1 \\\frac{1 - r^{n}}{1 - r} & \text{otherwise} \end{cases}\right)\)
อนุกรมเรขาคณิตแบบอนันต์
กรณีที่จำนวนพจน์ไม่มีที่สิ้นสุด (อนุกรมอนันต์) เราสามารถกำหนดใน ซิมไพ ได้โดยใช้อักษร oo ซึ่งแทนสัญลักษณ์ของอนันต์ (∞):
# อนุกรมเรขาคณิตแบบอนันต์
# เงื่อนไข: |r| < 1
infinite_sum = Sum(a * r**k, (k, 0, oo))
infinite_sum # ไม่ต้องหาผลรวม\(\displaystyle \sum_{k=0}^{\infty} a r^{k}\)
ซิมไพจะแสดงอนุกรมในรูปแบบ symbolic โดยยังไม่คำนวณผลรวม
อนุกรมเรขาคณิตแบบอนันต์จะมีผลรวมจำกัด ก็ต่อเมื่ออัตราส่วนร่วมมีค่าสัมบูรณ์น้อยกว่า 1 หรือ \(|r| < 1\) ซึ่งสามารถคำนวณผลรวมได้ด้วยคำสั่ง .doit() เช่นเดียวกัน
infinite_sum.doit() # หาผลรวม\(\displaystyle a \left(\begin{cases} \frac{1}{1 - r} & \text{for}\: \left|{r}\right| < 1 \\\sum_{k=0}^{\infty} r^{k} & \text{otherwise} \end{cases}\right)\)
4.1 เงินงวดสิ้นงวด (Ordinary Annuity)
Ordinary Annuity คือ การชำระเงินงวดเท่ากัน \(R\) ทุกสิ้นงวด เป็นระยะเวลา \(n\) งวด โดยมีอัตราดอกเบี้ย \(i\) คงที่ต่อช่วงเวลา
4.1.1 มูลค่าปัจจุบันของเงินงวดสิ้นงวด (Present Value of Ordinary Annuity)
มูลค่าปัจจุบันของเงินงวดสิ้นงวด คือ มูลค่าของชุดการรับเงินที่เกิดขึ้นอย่างสม่ำเสมอ ณ สิ้นแต่ละงวด โดยมีจำนวนงวดที่แน่นอน และใช้ดอกเบี้ยคงที่ในการคิดลด (discount) ย้อนกลับไปยังมูลค่าในปัจจุบัน
ในสถานการณ์ทั่วไป เงินงวดสิ้นงวดหมายถึง การรับเงินจำนวนคงที่ เช่น 1 หน่วย ในทุกๆ สิ้นงวด เช่น ทุกสิ้นเดือน หรือสิ้นปี โดยจะได้รับเป็นระยะเวลาต่อเนื่องกันทั้งหมด \(n\) งวด ซึ่งเงินที่ได้รับในแต่ละงวดในอนาคตจะมีค่าปัจจุบันน้อยลงตามหลักของมูลค่าเงินตามเวลา (Time Value of Money)
เพื่อให้สามารถเปรียบเทียบมูลค่าของชุดเงินงวดเหล่านี้กับมูลค่าเงินในปัจจุบันได้ เราจึงนำเงินแต่ละงวดในอนาคตมาคิดลดด้วยอัตราดอกเบี้ย \(i\) ต่อช่วงเวลา ซึ่งสามารถเขียนได้เป็นสมการต่อไปนี้:
\[a_{\overline{n}|i} = \frac{1 - v^n}{i} = \frac{1 - (1+i)^{-n}}{i}\] โดยที่:
\(a_{\overline{n}|i}\) คือ มูลค่าปัจจุบันของเงินงวดสิ้นงวด \(n\) งวด ที่ใช้อัตราดอกเบี้ย \(i\)
\(v = \frac{1}{1+i}\) คือ ค่าคิดลด (discount factor)
\(n\) คือ จำนวนงวดทั้งหมด
\(i\) คือ อัตราดอกเบี้ยต่อช่วงเวลา
ดังนั้น \[ \quad PV = R \cdot a_{\overline{n}|i}\]
4.2 มูลค่าอนาคตของเงินงวดสิ้นงวด (Future Value of Ordinary Annuity)
มูลค่าอนาคตของเงินงวดสิ้นงวด คือ มูลค่ารวมในอนาคตของเงินที่ฝากหรือสะสมไว้เป็นงวดๆ อย่างสม่ำเสมอ ณ สิ้นแต่ละงวด โดยใช้สมมติฐานว่าเงินแต่ละงวดที่สะสมไว้สามารถนำไปลงทุนต่อด้วยอัตราดอกเบี้ยคงที่ \(i\) ต่อช่วงเวลา และมีระยะเวลาการสะสมทั้งหมดจำนวน \(n\) งวด
ตัวอย่างของสถานการณ์เช่นนี้ ได้แก่ การออมเงินทุกสิ้นเดือนในบัญชีที่มีดอกเบี้ย หรือการฝากเงินเข้ากองทุนสะสมเป็นประจำในทุกสิ้นปี
การคำนวณมูลค่าอนาคตของเงินงวดสิ้นงวดสามารถใช้สมการดังนี้:
\[ s_{\overline{n}|i} =\sum_{k=1}^{n}(1+i)^{k-1} =\frac{(1 + i)^n - 1}{i} \]
โดยที่:
\(s_{\overline{n}|i}\) คือ มูลค่าอนาคตของเงินงวดสิ้นงวดจำนวน \(n\) งวด ที่ใช้อัตราดอกเบี้ย \(i\)
\(i\) คือ อัตราดอกเบี้ยต่อช่วงเวลา
\(n\) คือ จำนวนงวดทั้งหมด
หากแต่ละงวดมีจำนวนเงินงวด (เงินออมรายงวด หรือเงินจ่ายประจำงวด) เท่ากับ \(R\) มูลค่ารวมในอนาคต (Future Value) ของเงินทั้งหมดเมื่อสิ้นงวดสุดท้ายสามารถคำนวณได้จาก:
\[ FV = R \cdot s_{\overline{n}|i} \]
ซึ่งแปลว่า: เราสามารถหามูลค่าเงินที่สะสมไว้ทั้งหมด ณ สิ้นงวดสุดท้าย โดยการนำค่าสัมประสิทธิ์ \(s_{\overline{n}|i}\) คูณกับจำนวนเงินที่จ่ายหรือออมในแต่ละงวด
4.2.1 ความสัมพันธ์ระหว่าง \(a_{\overline{n}|i}\) และ \(s_{\overline{n}|i}\)
\[ s_{\overline{n}|i} = (1 + i)^n \cdot a_{\overline{n}|i} \]
ตัวอย่าง: นายสมศักดิ์จะฝากเงินปีละ 1,000 บาท เป็นเวลา 5 ปี โดยฝากทุกสิ้นปี และอัตราดอกเบี้ยร้อยละ 6 ต่อปี จะมีเงินมูลค่าปัจจุบันเท่ากับเท่าใด วาดรูป
 การคำนวณหาคำตอบด้วยซิมไพ
การคำนวณหาคำตอบด้วยซิมไพ
from sympy import symbols
# ประกาศตัวแปรพื้นฐาน
n, i = symbols('n i', positive=True)
# ใช้ชื่อแบบ LaTeX
a_ni = symbols('a_{\\overline{n}|i}', real=True)
a_ni = (1-(1+i)**-n)/i
a_ni\(\displaystyle \frac{1 - \left(i + 1\right)^{- n}}{i}\)
แทนค่าทั้งหมดลงไป
PV = 1000*a_ni.subs({i: 0.06, n: 5})
PV.evalf(6)\(\displaystyle 4212.36\)
วาดรูปหามูลค่าอนาคตที่เวลา 5 ปี
\[ FV = 1000 \cdot s_{\overline{5}|0.06} = 1000 \cdot \frac{(1 + 0.06)^5 - 1}{0.06} \approx 5,637.09 \]
# ประกาศตัวแปรพื้นฐาน
n, i = symbols('n i', positive=True)
# ใช้ชื่อแบบ LaTeX
s_ni = symbols('a_{\\overline{n}|i}', real=True)
s_ni = ((1+i)**n-1)/i
s_ni\(\displaystyle \frac{\left(i + 1\right)^{n} - 1}{i}\)
แทนค่าทั้งหมดลงไป
FV = 1000*s_ni.subs({i: 0.06, n: 5})
FV.evalf(6)\(\displaystyle 5637.09\)
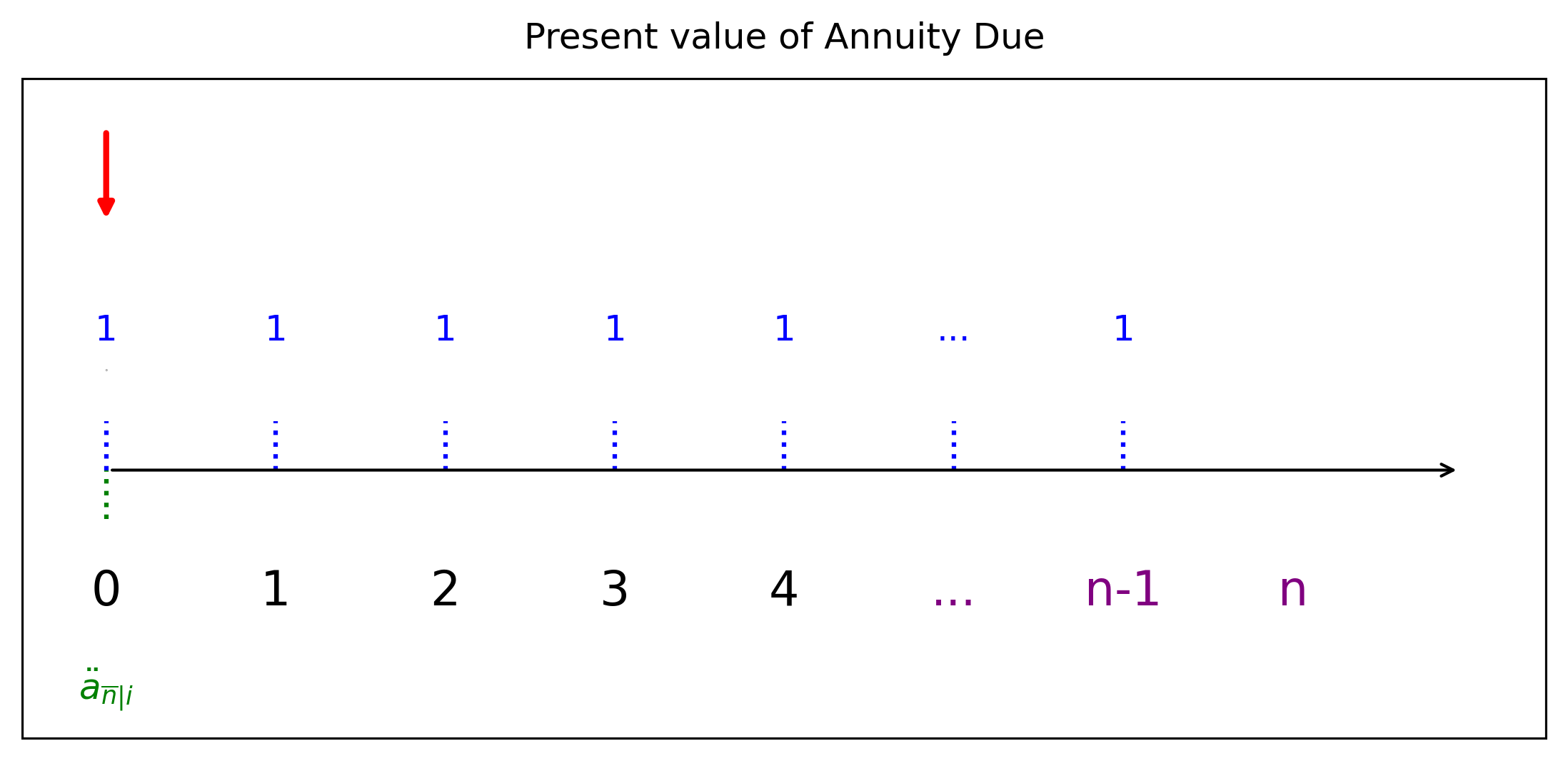
4.3 เงินงวดต้นงวด (Annuity Due)
เงินงวดต้นงวด (Annuity Due) คือชุดของการชำระเงินที่เกิดขึ้นอย่างสม่ำเสมอโดยเริ่มจ่าย ตอนต้นงวด แทนที่จะจ่ายตอนปลายงวดเหมือนเงินงวดทั่วไป (Ordinary Annuity) เช่น การจ่ายค่าเช่าบ้านในต้นเดือน หรือการชำระเบี้ยประกันล่วงหน้าต้นปี ถือเป็นตัวอย่างของเงินงวดต้นงวด
คุณสมบัติของเงินงวดต้นงวด
การชำระเงินแต่ละงวดจะเกิดขึ้น ทันทีที่เริ่มต้นงวด
แต่ละงวดมีเวลาในการทบต้นมากกว่าหนึ่งงวด เมื่อเทียบกับเงินงวดปลายงวด
ส่งผลให้ มูลค่าปัจจุบัน (PV) และ มูลค่าในอนาคต (FV) ของ Annuity Due สูงกว่า แบบปลายงวดที่มีเงื่อนไขเหมือนกัน
เมื่อบุคคลชำระเงินจำนวนเท่ากันในช่วง ต้นของแต่ละงวด ติดต่อกันเป็นเวลา \(n\) งวด เงินแต่ละงวดจะมีเวลาสะสมดอกเบี้ยนานกว่าการชำระปลายงวดหนึ่งช่วงเวลา ดังนั้น การคำนวณมูลค่าในอนาคตของเงินงวดต้นงวดจึงต้องคำนึงถึงช่วงเวลาที่แต่ละงวดได้รับดอกเบี้ย
ในกรณีที่เราต้องการหามูลค่าในอนาคตของเงินงวดต้นงวด ณ สิ้นงวดสุดท้าย (คือ ณ เวลาที่ \(n-1\)) เราสามารถพิจารณา มูลค่าปัจจุบัน ของการจ่ายเงินแต่ละงวดก่อน แล้วจึงสะสมดอกเบี้ยไปยังปลายงวด
มูลค่าปัจจุบันของเงินงวดต้นงวดสามารถแสดงได้โดยผลรวมของมูลค่าลดค่าของแต่ละงวด ซึ่งเริ่มตั้งแต่งวดแรก (งวดที่ 0) ไปจนถึงงวดที่ \(n-1\) โดยใช้ ตัวลดค่าปัจจุบัน (\(v = \frac{1}{1+i}\)) สำหรับอัตราดอกเบี้ย \(i\) ต่อหนึ่งงวด จากแนวคิดนี้ เราสามารถเขียนสมการได้ดังนี้: \[ \ddot{a}_{\overline{n}|i} = \sum_{k=0}^{n-1}{v^k}, \quad \text{โดยที่ } v = \left(\dfrac{1}{1+i}\right) \] สมการข้างต้นสามารถจัดรูปใหม่เพื่อให้ง่ายต่อการคำนวณ: \[\ddot{a}_{\overline{n}|i} = \dfrac{v(1 - v^{n-1})}{i} = v \cdot a_{\overline{n-1}|i}\]
4.3.1 มูลค่าในอนาคตของเงินงวดต้นงวด (Future Value of Annuity Due)
เงินงวดต้นงวด (Annuity Due) คือการชำระเงินในแต่ละงวดที่เกิดขึ้น ตอนต้นงวด แทนที่จะเป็นปลายงวดเหมือนในกรณีของเงินงวดทั่วไป (Ordinary Annuity) ตัวอย่างเช่น การชำระค่าเช่าที่ต้องจ่ายล่วงหน้าก่อนเริ่มเดือน หรือเบี้ยประกันที่ชำระต้นปี
ในการวิเคราะห์ทางการเงิน หากเราต้องการทราบ มูลค่าในอนาคต ของเงินงวดต้นงวดเมื่อสิ้นสุดงวดสุดท้าย จำเป็นต้องคำนึงว่าเงินแต่ละงวดมีระยะเวลาสะสมดอกเบี้ยมากกว่าปกติหนึ่งงวด เพราะถูกจ่ายล่วงหน้าตั้งแต่ต้นงวด
ด้วยเหตุนี้ การคำนวณมูลค่าในอนาคตของเงินงวดต้นงวดจึงใช้หลักการเดียวกับเงินงวดปลายงวด แต่มีการปรับให้สะท้อนว่าเงินแต่ละงวดได้สะสมดอกเบี้ย นานขึ้นหนึ่งช่วงเวลา เมื่อเทียบกับเงินงวดปลายงวด จากหลักการข้างต้น สามารถแสดงสมการได้ดังนี้: \[\ddot{s}_{\overline{n}|i} = \sum_{k=1}^{n}(1+i)^{k} = (1+i)\cdot \frac{(1+i)^n - 1}{i} = (1+i)\cdot s_{\overline{n}|i}\]
สมการนี้แสดงว่า: มูลค่าในอนาคตของเงินงวดต้นงวดเท่ากับ มูลค่าในอนาคตของเงินงวดปลายงวด (Ordinary Annuity) คูณด้วย \((1+i)\) ซึ่งแสดงถึงการสะสมดอกเบี้ยล่วงหน้าหนึ่งงวดในทุกการชำระเงิน
ตัวอย่าง นายสมชายวางแผนออมเงินจำนวน 1,000 บาท ทุกต้นเดือน เป็นเวลา 5 เดือนในบัญชีออมทรัพย์ที่ให้ดอกเบี้ยร้อยละ 5 ต่อเดือน (คิดแบบทบต้นรายเดือน)
จงหามูลค่าปัจจุบันของแผนการออมนี้ ณ เวลาปัจจุบัน
จงหามูลค่าในอนาคตของเงินออมทั้งหมด ณ สิ้นเดือนที่ 5
วาดรูป
มูลค่าปัจจุบัน (Present Value): \[1000\ddot{a}_{\overline{5}|i} =1000( \sum_{k=0}^{5-1} v^k), \quad \text{โดย } v = \frac{1}{1+i},~ i=\dfrac{i^{(12)}}{12}=.05/12\] มูลค่าในอนาคต (Future Value) ณ สิ้นเดือนที่ 5 \[1000\ddot{s}_{\overline{5}|i} = 1000(\sum_{k=1}^{5} (1+i)^{k}),~ i=\dfrac{i^{(12)}}{12}=.05/12\] จะใช้ซิมไพหาคำตอบใช้การคำนวณด้วยสูตรผลรวมโดยตรง
from sympy import Sum
# ประกาศตัวแปรพื้นฐาน
i, k, n, v= symbols('i k n v', positive=True)
# ใช้ชื่อแบบ LaTeX
adot_ni = symbols('\\ddot{a}_{\\overline{n}|i}', real=True)
adot_ni = 1000*Sum(v**k, (k, 0, n - 1))
adot_ni.doit()\(\displaystyle 1000 \left(\begin{cases} n & \text{for}\: v = 1 \\\frac{1 - v^{n}}{1 - v} & \text{otherwise} \end{cases}\right)\)
# ดอกเบี้ยต่อเดือน .05/12
PV = adot_ni.subs({v: 1/(1+.05/12), n: 5})
PV.evalf(6)\(\displaystyle 4958.68\)
หามูลค่าสะสม วาดรูป
# สร้างนิพจน์สำหรับมูลค่าในอนาคต (Annuity Due)
# ใช้ชื่อแบบ LaTeX
sdot_ni = symbols('\\ddot{s}_{\\overline{n}|i}', real=True)
sdot_ni = 1000*Sum((1+i)**k, (k, 1, n))
sdot_ni.doit()\(\displaystyle - \frac{1000 \left(i - \left(i + 1\right)^{n + 1} + 1\right)}{i}\)
# ดอกเบี้ยต่อเดือน .05/12
FV = sdot_ni.subs({i: .05/12, n: 5})
FV.evalf(6)\(\displaystyle 5062.85\)
ก่อนที่จะมีการใช้คอมพิวเตอร์ช่วยในการคำนวณ สูตรที่ผ่านมามีความสำคัญมาก เพราะทำให้การคำนวณมีความง่ายมากกว่าที่ใช้การคำนวณตรงโดยใช้ผลรวมของมูลค่าปัจจุบันทั้งหมด หรือผลรวมของมูลค่าอนาคตทั้งหมด ในหนังสือเล่มนี้ก็ยังคงใช้วิธีคำนวณโดยการจัดรูปให้เข้าสูตร เพื่อคงความสวยงามทางคณิตศาสตร์เอาไว้
จากหัวข้อที่ผ่านมา เราสามารถสังเกตุได้ว่า ถ้าเราสามารถเห็นรูปแบบการจ่ายที่มีโครงสร้างสร้างแบบการจ่ายรายงวด เราสามารถเขียนสมการแห่งมูลค่าใหม่ได้
ตัวอย่าง จงเขียนสมการแห่งมูลค่าจากแผนภาพต่อไปนี้
รายงวดสีเขียวสามารถเขียนให้เป็น \(1000s_{\overline{5}|i}\) ณเวลาที่ 4 และ รายงวดสีน้ำเงินสามารถเขียนได้เป็น \(1000s_{\overline{5}|i}\) ณ เวลาที่ 10 วาดรูปใหม่ได้เป็น
หลังจากนั้น กำหนดจุดที่ต้องการเพื่อเขียนสมการแห่งมูลค่าได้ทันที
สมมุติเลือก ที่จุด 0 จงหาอัตราดอกเบี้ยรายปี ที่ทำให้สมการแห่งมูลค่านี้เป็นจริง \[1000v^4s_{\overline{5}|i}=1200v^{10}s_{\overline{5}|i}\]
i,v = symbols('i v', positive = True, real=True)
s_5i = symbols('s_{\\overline{5}|i}', real=True)
v =1/(1+i)
s_5i=((1+i)**5-1)/i
eq =Eq(1000*v**4*s_5i,1200*v**10*s_5i) #. สร้างสมการ
eq # แสดง equation of value\(\displaystyle \frac{1000 \left(\left(i + 1\right)^{5} - 1\right)}{i \left(i + 1\right)^{4}} = \frac{1200 \left(\left(i + 1\right)^{5} - 1\right)}{i \left(i + 1\right)^{10}}\)
แก้สมการด้วยคำสั่ง solve()
solutions = solve(eq,i)
# แสดงคำตอบ
solutions[0].evalf(4)\(\displaystyle 0.03085\)
สมการแห่งมูลค่าจะเป็นจริงเมื่ออัตราดอกเบี้ยเท่ากับ 3.09%
ตัวอย่าง ฝากเงินครั้งละ 10,000 ทุกต้นปีเป็นจำนวน 10 ครั้ง ถ้าธนาคารให้อัตราดอกเบี้ย 5% ต่อปี ต้องใช้เวลาเท่าไหร่ ถึงจะมีเงินสะสมเท่ากับ 200,000 บาท
วาดรูป
 จัดรูปใหม่จะได้
จัดรูปใหม่จะได้
 สมการแห่งมูลค่าคือ \[10000v^9s_{\overline{10}|i}=200000v^t\]
สมการแห่งมูลค่าคือ \[10000v^9s_{\overline{10}|i}=200000v^t\]
i, v, t = symbols('i v t', positive = True, real=True)
s_10i = symbols('s_{\\overline{10}|i}', real=True)
i =0.05
v =1/(1+i)
s_10i=((1+i)**10-1)/i
eq =Eq(1e4*v**9*s_10i,2e5*v**t) #. สร้างสมการ
eq # แสดง equation of value\(\displaystyle 81078.2167564406 = 200000.0 {0.952380952380952}^{t}\)
แก้สมการด้วยคำสั่ง solve()
solutions = solve(eq,t)
# แสดงคำตอบ
solutions[0].evalf(4)\(\displaystyle 18.51\)
4.4 เงินรายงวดจ่าย \(m\) ครั้งต่อปี (Annuities Payable m Times per Year)
ในทางคณิตศาสตร์การเงิน “annuities payable m times per year” หมายถึงเงินรายงวดที่จ่ายเป็นจำนวนครั้งเท่ากันในแต่ละปี โดยแบ่งปีออกเป็น \(m\) งวดเท่า ๆ กัน เช่น รายเดือน (\(m = 12\)) รายไตรมาส (\(m = 4\)) หรือรายครึ่งปี (\(m = 2\))
การวิเคราะห์มูลค่าปัจจุบัน (present value) และมูลค่าอนาคต (accumulated value) ของอนุกรมประเภทนี้ ต้องใช้ดอกเบี้ยต่อช่วงจ่าย (periodic interest rate) และจำนวนงวดทั้งหมดในรูปของ \(mn\)
สัญลักษณ์ที่ใช้:
\(i\): อัตราดอกเบี้ยรายปีที่จ่ายสิ้นปี (effective annual rate)
\(i^{(m)}\): อัตราดอกเบี้ยที่ใช้ต่อแต่ละงวดเมื่อมี \(m\) งวดต่อปี (i.e., nominal rate compounded m times)
\(\frac{i^{(m)}}{m}\): อัตราดอกเบี้ยต่อหนึ่งงวดย่อย
\(n\): จำนวนปีที่จ่ายรายงวด
\(mn\): จำนวนงวดทั้งหมด
\(\ddot{a}_{\overline{n}|i}^{(m)}\): มูลค่าปัจจุบันของ annuity-immediate ที่จ่าย \(m\) ครั้งต่อปี เป็นเวลา \(n\) ปี
4.4.1 มูลค่าปัจจุบันของ Annuity-immediate ที่จ่าย \(m\) ครั้งต่อปี:
\[ \ddot{a}_{\overline{n}|i}^{(m)} = \frac{1 - v^n}{d^{(m)}} \quad \text{where} \quad d^{(m)} = m \left( 1 - v^{1/m} \right) \]
หรือในรูปแบบที่พบได้บ่อยกว่า: \[ a_{\overline{n}|i}^{(m)} = \frac{1 - v^{n}}{i^{(m)}/m} \quad \text{with} \quad v = \frac{1}{1+i} \]
4.4.2 มูลค่าอนาคต (Sinking Fund Formula):
\[ s_{\overline{n}|i}^{(m)} = \frac{(1 + i)^n - 1}{i^{(m)}/m} \]
4.4.3 ตัวอย่างเชิงคำอธิบาย:
หากมีการจ่ายเงิน 100 บาททุกเดือน เป็นเวลา 5 ปี โดยมีอัตราดอกเบี้ย 6% ต่อปี ทบต้นรายเดือน (\(m = 12, i = 0.06\)) จะสามารถคำนวณมูลค่าปัจจุบันของ annuity นี้ได้โดยใช้:
\[ \ddot{a}_{\overline{5}|0.06}^{(12)} = \frac{1 - (1 + 0.06)^{-5}}{0.06/12} \]
ซึ่งสะท้อนถึงมูลค่าปัจจุบันของการจ่ายเงิน 60 งวด (5 ปี × 12 เดือน)